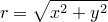link to this article

Abstract

mkheightmap is a tool contained in picogen [0] to create heightmaps [1] with the help of a small, user written program in a lisp-like syntax, called Height-Slang.

Part 1 of this article series focuses on the absolute basics. Part II will give an overview about more advanced functions and control-flow, Part III will introduce the concept of configurable functions and shows the mighty LayeredNoise-function.

Hello World

Open a terminal. If you haven't picogen in /usr/bin, then dive into the directory where picogen currently is. Then type this in:

picogen mkheightmap -Lhs "x" -p

Et voila, you've just created your first (not too fascinating) heightmap:

Now number 2 (focus your eyes on what is written after '-Lhs'):

picogen mkheightmap -Lhs "y" -p

Now think about what has happened. The whole code for our first heightmap looked like "x", and we've seen increasing height (with low being black, high being white) from the left to the right. For the second map we've changed the code to "y", and we've seen increasing height from the top to the bottom. Combining those facts now is all and nothing: The value of the expression "x" is simply the canonical x-coordinate on the image, from left to right, from 0.0 to 1.0; "y" is then from top to bottom, from 0.0 to 1.0.

A more elaborate Hello World

This time, type in the following (the parameter '-n' scales all height values so that they fit in [0..1)):

picogen mkheightmap -Lhs "(sin (* x 50))" -p -n

If the code looks a bit weird to you now, fear not. I haven't invented it, it's borrowed from LISP [2], and it's really very easy. Think of it like everything is a function, and with a statement like

(* x 50)

you call the multiply-function, with x and 50 being the parameters to it.

It is that every parameter to a function can be a function call, too. Hence we can construct more complex functions, like:

(sin (* x 50))

This calls the sine-function, with (* x 50) being it's parameter, so we take the 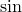of the value of 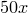. Naturally, the outermost expressions are evaluated last, in the sense that in our example 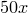is calculated first, and then the sine is taken.

Knowing this, if you're still here and not hacking Height-Slang into your terminal, try out the next one:

picogen mkheightmap -Lhs "(sin (* 20 (sqrt (+ (^ x 2) (^ y 2)))))" -p -n

If that looks like horror to you, practice is all. Look at the innermost expressions:

(^ x 2)
  and
(^ y 2)

The function 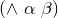simply means 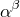, so in our example (^ x 2) simply squares x.

The next thing to inspect is the following expression:

(+ (^ x 2) (^ y 2))

Here we simply add together the squared values of x and y. Then:

(sqrt (+ (^ x 2) (^ y 2)))

Where 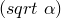takes the square root of the expression 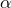. Does that look familiar? Correct ([3]):

At next, we multiply what we have calculated so far by a factor of 20 (to get more waves in the resulting image):

(* 20 (sqrt (+ (^ x 2) (^ y 2))))

It becomes easier, not? And we're getting ready with this section. Just the remaining call to the sine-function has to be accomplished. I'll leave that to you as an exercise (not that it has not already been written sooner).

Exercise

Now extend the expression "(sin (* 20 (sqrt (+ (^ x 2) (^ y 2)))))" so that the resulting heightmap becomes (just look at it, don't read the solution yet):

solution

Simply add a subtraction by 0.5 to both x, y:

        (sin (* 20
                (sqrt (+ (^ (- x 0.5) 2)
                         (^ (- y 0.5) 2)
                      )
                )
             ))
        

Now play a bit around with the expression where at the moment is "20". A damn cool factor is: "(/ 100 (^ y x))" or :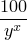

        (sin (* (/ 100 (^ y x))
                (sqrt (+ (^ (- x 0.5) 2)
                         (^ (- y 0.5) 2)
                      )
                )
             ))
        

Conclusion

Now get a terminal and hack a bit, the Height-Slang Reference [4] contains a list of all available functions.